-1-

很多人认为数学没用几何学英语，或者用处不大，在学校学的三角函数、二次方程在现实生活中应用不了。一般来说，他们在购物时只会使用一些加减法。这种想法就像微积分是牛顿和莱布尼茨发明的一样错误。

数学是物理学的基础，物理学的发展促进了我们的技术。毫无疑问，古往今来，大多数发明家首先是物理学家。我们的文明发展到今天，离不开数学。航海、天文学、矿山建设等许多课题都依赖于数学的发展才能深入研究。

有一个很典型的故事，一个物理系的学生问他的老师：“为什么近100年来物理学没有什么惊天动地的成就？” 老师想都没想就直接回答：“因为数学还没有发展起来。”虽然这只是一个故事，真假难辨，但已经可以说明数学的重要性了。现实生活中应用最广泛的数学是微积分。

微积分的出现解决了两个一直困扰着人们的问题：第一个是如何计算曲线上任意一点的切线，即微分；二是如何计算任何面积的面积，即积分。所以微积分是微分学和积分学的总称。

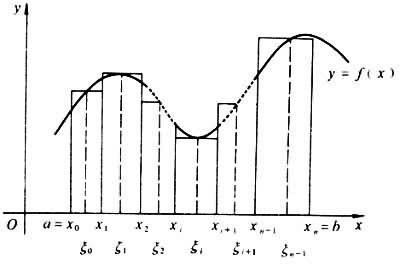
微积分原理示意图

说到微积分，很多人都头疼。但是没有微积分就不能学习数学。我国有句古话，“工欲善其事，必先利其器”。微积分是数学家手中的“利器”。许多研究都基于微积分。，其重要性不言而喻。说到微积分，很多人认为是函数。事实上，微积分是一个综合概念，主要包括极限、微分、积分及其应用。其中微积分包括导数的计算，是关于变化率的一套理论，积分包括计算积分的运算。说到微积分，很多人第一时间会想到牛顿和莱布尼茨，认为这两个人发明并创造了微积分。事实上，事实并非如此。事实上，微积分是几代数学家不断努力和研究的结果。经过很长时间的发展演变才形成。

牛顿肖像↑

莱布尼茨肖像 ↑

-2-

微积分思想的萌芽甚至可以追溯到公元前7世纪。古希腊科学家泰勒斯在他对球的面积、体积和长度的研究中包含了微积分思想。阿基米德在抛物线下圆弧面积、球体和球冠面积、螺线下面积、双曲线旋转得到的体积的研究和求解中也隐含了现代积分的思想。三国时期，刘徽研究了切圆术，也研究了积分。遗憾的是，在微积分发展最快的中世纪，我国正处于封闭的明清时期，我们无法与世界其他数学家一起狂欢。

到了十七世纪，有许多科学问题需要解决，这些问题成为促使微积分创立的因素。它归结为大致四种主要类型的问题：

第一类是研究运动时直接出现的问题，即求瞬时速度的问题。

第二类问题是求曲线切线的问题。

第三类问题是求函数的最大值和最小值。

第四类题是求曲线的长度、曲线围成的面积、曲面围成的体积、物体的重心、体积作用较大的物体的重力在另一个物体上。

17世纪许多著名的数学家、天文学家、物理学家都为解决上述问题做了大量的研究工作，如法国的费马、笛卡尔、罗伯瓦尔、笛沙格；罗，瓦利斯；德国的开普勒；意大利的卡瓦列里等人提出了许多非常成功的理论。对创建微积分做出了贡献。

十七世纪下半叶，在前人工作的基础上，英国伟大的科学家牛顿和德国数学家莱布尼茨在本国独立研究并完成了微积分的创立，尽管这只是非常初步的工作。他们最大的成就是把两个看似无关的问题联系起来，一个是切线问题（微分学的中心问题），一个是求积问题（积分学的中心问题）。

牛顿和莱布尼茨建立微积分的出发点是直观的无穷小量，所以这门学科早期也被称为无穷小分析，这就是数学中分析分支名称的来源。牛顿的微积分研究侧重于运动学，而莱布尼茨的研究侧重于几何学。

微积分的建立极大地促进了数学的发展。过去很多初等数学难的问题，用微积分就可以轻松解决，可见微积分的非凡威力。

需要指出的是，历史上任何一个重大理论的完成都需要一段时间，牛顿和莱布尼茨的著作也很不完善。他们在无限量和无穷小量的问题上意见不一，而且很含糊。牛顿无穷小量有时为零，有时不为零而是有限小量；莱布尼茨无法自圆其说。这些根本性缺陷最终导致了第二次数学危机。

直到19世纪初，以柯西为首的法国科学院的科学家们对微积分理论进行了认真的研究，建立了极限理论，并经德国数学家维斯特拉斯进一步完善，使极限理论成为一个A坚实的微积分基础。直到那时微积分才进一步发展。任何新的、有前途的科学成果都会吸引大量的科学工作者。在微积分的历史上，也有一些这样的明星：瑞士的雅各布·伯努利和他的弟弟约翰·伯努利，欧拉，法国的拉格朗日，柯西……欧氏几何也好，古代和中世纪的代数就是一种常数数学，而微积分是真正的变量数学，是数学的一次伟大革命。微积分是高等数学的主要分支。它不仅限于解决力学中的变速问题。它驰骋于近现代科技领域，建立了无数丰功伟绩。

一些数学家，包括科林·麦克劳克林，曾尝试使用无穷小进行证明，但直到 150 多年后才得以实现。在Augustin-Louis Cauchy 和Karl Weierstrass 的努力下，终于实现了对无穷小符号的避免。终于奠定了分化与融合的基础。在 Cauchy 的工作中，我们看到了许多基本论点，包括通过连续性定义无穷小，以及用于定义微分的 (ε,δ)-limit 定义的不太精确的版本。魏尔斯特拉斯推导总结了极限的概念，避开了无穷小。在魏尔斯特拉斯之后几何学英语，微积分通常基于极限而不是无穷小。伯恩哈德黎曼使用这些概念给出了积分的严格定义。在这段时期，

极限并不是微积分基础的唯一推导，例如使用亚伯拉罕·罗宾逊的非标准分析得出的推导。罗宾逊在1960年前后所做的推导继承了牛顿-莱布尼茨最初的概念，应用数理逻辑将实数系扩展到无穷小和无穷大。得到的结果是一个超实数，可以应用莱布尼兹型微积分规则。

当时，牛顿和莱布尼茨发明微积分也引起了轩然大波。英国皇家科学院支持当地的牛顿，而欧洲大陆的其他一些国家则推崇德国的布莱尼茨。这场对峙持续了一年。几个世纪以来，导致微积分的发展停滞不前。事实上，牛顿和莱布尼茨各自进行了独立的研究，有趣的是两人在相似的时间完成了自己的研究。牛顿创造微积分比莱布尼茨早10年左右，但莱布尼茨比牛顿早三年正式发表微积分理论。时间先后顺序并不能说明很多问题微积分的历史和应用，就像计算机一样，想想就令人兴奋，而且虽然都是学微积分的，但是研究方向其实不一样。牛顿在1671年写下了《流利无限级数》几何学英语，指出变量是由点、线、面的连续运动产生的。他在流动的艺术中提出的中心问题是：知道连续运动的路径，求出给定时刻的速度，或者在已知运动速度的情况下，求出给定时间内行进的距离。莱布尼茨于 1684 年发表了现在被认为是世界上最早的微积分文献。这篇文章的标题相当抢眼，叫做“求极大值、极小值和切线的新方法，也适用于分数和无理数，以及这种新方法的精彩计算类型”。这篇看似潦草的文章包含了现代微分符号和基本微分定律。1686年，莱布尼茨发表了第一篇积分学论文。我们今天使用的微积分常用符号是莱布尼茨当时选择的符号。简单来说，牛顿学微积分的重点是运动学，而莱布尼茨的重点是几何学。他们最大的成就是将两个看似无关的问题结合在一起：切线问题，微积分的核心问题，以及求积问题，微积分的核心问题。

calculus的英文单词是Calculus，不是英语，而是拉丁文，原意是小石头。看到这里，很多人可能不明白，谁愿意用这么平淡无奇的东西来命名这么高水平的新兴学科？答案是莱布尼茨。在古代，人们用小石子作为计算工具，久而久之，小石子就代表了一种计算方式。因此，莱布尼茨巧妙地采用了这个传统名称来命名新兴事物。此外，莱布尼茨还用拉长的S表示积分，用d表示差。这两个词也源自拉丁语。而牛顿创造了 Fluxion（通量）一词来表示导数。并发现了微积分定理的第一个版本。所以很难说谁对微积分的发明贡献更大。现在，人们普遍认为，牛顿和莱布尼茨建立了自己的体系，彼此之间没有交流，更谈不上抄袭。这是作者非常正确和健康的学术心态。与其纠结于这种难以发现的历史问题，不如多做科学研究，为建设明天的数学大厦贡献一份力量。这是每一个学者都应该关心的。

-3-

微分应用包括极限速度、加速度、曲线斜率、优化等。积分应用包括面积、体积、弧长、质心、功​​和压力。更高级的应用包括幂级数和傅里叶级数等。

微积分有助于更精确地理解空间、时间和运动的本质。几个世纪以来，数学家和哲学家一直在为除以零或无穷大的悖论而苦恼。在研究运动和面积时经常会出现这些问题。古希腊哲学家埃利亚的芝诺给出了这个悖论的几个著名例子。微积分，尤其是极限级数和无限级数，提供了解决这个悖论的工具。

微积分的发展和应用几乎影响了现代生活的各个领域。它与大多数科学分支密切相关，包括精算学、计算机、统计学、工程、商业、医学、人口统计学，尤其是物理学；经济学也经常使用微积分。几乎所有现代技术，如建筑、航空等，都使用微积分作为基本的数学工具。微积分允许数学将变量和常数相互转换，允许我们在知道另一种方式时推导一种方式。

物理学大量使用微积分。所有经典力学和电磁学都与微积分密切相关。已知密度的物体的质量、动摩擦力、保守力场的总能量都可以通过微积分计算出来。例如，将微积分应用于牛顿第二定律：史料一般将衍生品称为“变化率”。物体动量的变化率等于在同一方向上施加在物体上的力。今天常用的表达方式是用它代替微分，因为加速度要么是速度的导数，要么是位置矢量的二阶导数。知道一个物体的加速度几何学英语，我们就可以推导出它的路径。

麦克斯韦的电磁学和爱因斯坦的广义相对论都应用了微分。化学使用微积分来计算反应速率、放射性衰变。生物学使用微积分来计算种群动态，并输入繁殖和死亡率来模拟种群变化。

微积分可以与其他数学分支交叉混合。例如，混合线性代数以找到范围内数字序列的“最佳”线性近似值。它还可以在概率论中用于确定由假设的密度方程产生的连续随机变量的概率。在解析几何中方程的形象研究中，微积分可以求最大值、最小值、斜率、凹度、拐点等。

格林公式将闭合曲线上的线积分与由 的平面区域界定并在其上的二重积分连接起来。它被设计为用于测量不规则表面面积的测平面工具。例如，它可以在设计时计算不规则花瓣床、游泳池的面积。

在医学领域，微积分可以计算出血管的最佳分支角度，使血流量最大化。通过药物在体内的衰减数据，微积分可以推算出剂量。在核医学中，它可以模拟治疗肿瘤的辐射传递。在经济学中，微积分可以通过计算边际成本和边际利润来确定最大收益。

微积分还用于求方程的近似值；在实践中，它用于求解微分方程和计算相关问题，如牛顿法、不动点循环、线性近似等。例如，航天器在零重力环境下使用欧拉法获得近似曲线。

很多人不学数学，不懂数学，但不得不承认微积分确实有用，我们生活的物质世界就是靠这样的理论支撑的。

未经允许不得转载：阿卡索学习网 - 英语学习培训机构网站！ > 微积分的历史和应用，就像计算机一样，想想就令人兴奋